无符号数、有符号数（补码）
浮点型、IEEE

整形

补码和无符号数

关系

补码和无符号数关系
- 无符号数和有符号数并列。
- 有符号数的一种表示形式是补码
转化(位数为[w-1,0])
- 补码 -> 无符号
  - T2U(x) = x + 2^w (x<0)
  - T2U(x) = x (x>=0)
- 无符号 -> 补码
  - U2T(u) = u (u<=TMax)
  - U2T(u) = u-2^w (u>TMax)
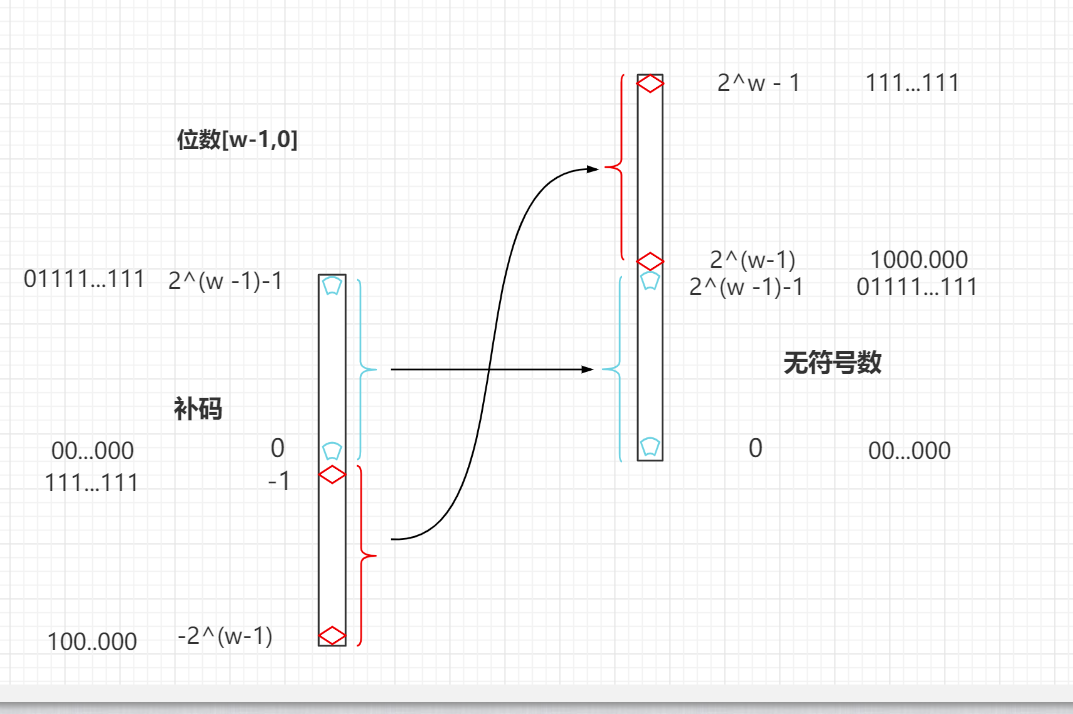
补码表示范围
- 前提：总共有n位。位数分别是[n-1,0]。也即从0开始，最高位是n-1
- [-2^(n-1),2^(n-1)-1];（下例中就是[-2^7 , 2^7-1];）
无符号数表示范围
- 前提：总共有n位。位数分别是[n-1,0]。也即从0开始，最高位是n-1
- [0,2^n-1]（下例中就是[0 , 2^8-1];）
首位的符号位可以看作是一个带正/负号的数值位。
- 当首位符号位为0时，该补码形式所表示的真值就是[6,0]位的和 + 首位0；首位符号位为1时，该补码形式所表示的真值就是就是首位-2^7 + [6,0]位的数值位之和。
- 补码与原码转化。原码 = ~补码+1。不用记，无所谓。求真值用上面的方法就好。

例子：总共8位。[7,0]

有符号数补码形式。[-2^7 , 2^7-1];

7 6 5 4 3 2 1 0

0 1 1 1 1 1 1 1     //  2^7 - 1 = 127
...
0 0 0 0 0 0 0 1     
0 0 0 0 0 0 0 0     //  0
1 1 1 1 1 1 1 1     //  -2^7 + 2^6 + 2^5 + ... + 2^0 = -1;
...
1 0 0 0 0 0 0 1     //  -2^7 + 1 = -127（该二进制数据对应的真值）
1 0 0 0 0 0 0 0     //  -2^7 = -128（该二进制数据对应的真值）

无符号数。[0,255]

7 6 5 4 3 2 1 0

7 6 5 4 3 2 1 0
1 1 1 1 1 1 1 1     //  2^8-1=255
1 1 1 1 1 1 1 0     //  254
...
0 0 0 0 0 0 0 1     //  2^0 = 1;
0 0 0 0 0 0 0 0     //  0

从min到max是个循环

例子

无符号 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 …

补码 0 1 2 3 -4 -3 -2 -1 0 1 2 3…

有符号数（补码）的溢出：是由正变负，由负变正
无符号数的溢出：由正变0，由0变正。（无符号数的溢出就是取模）

左移导致溢出。举例有符号补码

int main()
{
    int x = 1;  //  有符号数 补码形式表示
    for(int i=0;i<=33;++i)
    {

        cout<<(x<<i)<<endl;
        for(int j=31;j>=0;--j)
        {
            cout<<(((x<<i)>>j)&1);
        }
        cout<<endl;
    }
}

shc@shc-virtual-machine:~/code/try$ ./test.out
1
00000000000000000000000000000001
2
00000000000000000000000000000010
4
00000000000000000000000000000100
8
00000000000000000000000000001000
16
00000000000000000000000000010000
32
00000000000000000000000000100000
64
00000000000000000000000001000000
128
00000000000000000000000010000000
256
00000000000000000000000100000000
512
00000000000000000000001000000000
1024
00000000000000000000010000000000
2048
00000000000000000000100000000000
4096
00000000000000000001000000000000
8192
00000000000000000010000000000000
16384
00000000000000000100000000000000
32768
00000000000000001000000000000000
65536
00000000000000010000000000000000
131072
00000000000000100000000000000000
262144
00000000000001000000000000000000
524288
00000000000010000000000000000000
1048576
00000000000100000000000000000000
2097152
00000000001000000000000000000000
4194304
00000000010000000000000000000000
8388608
00000000100000000000000000000000
16777216
00000001000000000000000000000000
335544321
00000010000000000000000000000000
67108864
00000100000000000000000000000000
134217728
00001000000000000000000000000000
268435456
00010000000000000000000000000000
536870912
00100000000000000000000000000000
1073741824
01000000000000000000000000000000
-2147483648
10000000000000000000000000000000

如果x是unsigned int的话 那么就是
2147483648
10000000000000000000000000000000

转化

有符号数与无符号数发生比较/运算时，有符号数会先被转化为无符号数
- signed(two’s complement) -> unsigned

例子

#define DELTA sizeof(char)
int i;

//  死循环
i-sizeof(char) 得到一个unsigned
// 因为sizeof 返回 size_t ，是unsigned
for(i=CNT;i-DELTA>=0;--i)
{
  //...
}

例子。错把无符号数当作有符号数。递减得到INT_MAX

//  死循环。不会终止。
for( unsigned i = 4 ; i>=0 ; --i )
{
  ...
}
00000000000000000000000000000100  4
...
00000000000000000000000000000001  1
00000000000000000000000000000000  0
11111111111111111111111111111111  signed : -1 / unsigned : 2^32-1
11111111111111111111111111111110  signed : -2 / unsigned : 2^32-2
...
10000000000000000000000000000000  signed : -2^31 / unsigned : 2^32
01111111111111111111111111111111  signed : 2^31-1 / unsigned : 2^31-1
01111111111111111111111111111110  signed : 2^31-2 / unsigned : 2^31-2

printf并没用使用变量的任何类型信息，只是根据%d %u %x这样的指示符来按照指示将变量底下的字节以相应形式输出。

//  32位
int x = -1;                   11111...1111
unsigned u = 2147483648;      10000...0000

printf("x=%u=%d\n",x,x);
printf("u=%u=%d\n",u,u);

x = 4294967295 = -1;
u = 2147836848 = -2147836848

有符号数转无符号数对于标准的算数运算并无多大差异，但对于<>比较运算开输送，就会导致非直观的结果。

// 表达式                              类型             结果
-2147483647-1 == 2147836848U         unsigned            1
-2147483647-1U < 2147836847          unsigned            0      
// 1000...0000 U < 0111...1111  
-2147483647-1U < -2147483647         unsigned            1
// 1000...0000 U < 1000...0001

符号扩展

符号的扩展发生了什么（符号扩展在由小类型到大类型时发生）
有符号数：补码的符号扩展。
- 复制符号位：向高位拿了一个新位用作符号位，新符号位的权重是原符号位的2倍，把这个原先的符号位用作正的数值位。
- 这样并不改变这些数值位的总和；也即并不改变数（真值）的大小
- 将各个权值位相加，可得补码对应的真值。
  1
  2
  3
  5 4 3 2 1 0
  1 1 1 0 : -8 + 4 + 2 = -2
  1 1 1 1 0 : -16 + 8 + 4 + 2 = -2

无符号数：0扩展

1
2
3

5 4 3 2 1 0
    1 1 1 0   : 8 + 4 + 2 = 14
  0 1 1 1 0   : 8 + 4 + 2 = 14

截断

截断会导致数变化很大。例如补码被截断就有可能一正一负，无符号数被截断就是取模。
无符号数。直接模
1
2
1011 // 8+2+1=11
011 // 3 = 11%8

有符号数。补码形式。

11011   //  -16+8+2+1=-5
->
1011   //  -8+2+1=5
没变。是因为从1011到11011可以看作是符号位拓展。
-------------------------------------------
10011   //  -16+2+1=-13
->
0011   //  2+1=3
3 != -13%16

无论溢出的那个下一个高位有什么，我们都假装看不到并舍弃。只拿低位的[n-1,0]位当作我获得的结果，编译器对这个过程也不会有任何warning

移位

补码右移：算数移位。copy符号位
补码左移：直接移，低位补0
无符号数右移：逻辑右移。高位补0
无符号数左移：逻辑左移。低位补0
总共w位，如果右移k位，且k>=w位，那么结果是:
- 大多数机器中都是这样做：实际位移量是 k mod w。
- C标准中规避了说明这种情况下如何做，因此这种行为对C程序来说没有保证。

习题

六进制中从8到F的最高有效位为1，记住这一点就会发现十六进制表示二进制更方便

int fun1(unsigned word){
              //  逻辑左移 低位补0
  return (int)( (word<<24) >> 24 );
                        //  逻辑右移 高位补0
}

int fun2(unsigned word){
              //  算数左移 低位补0
  return ( (int)word<<24 ) >> 24;
                        //  算数右移 高位补x[w-1]
}

w                   fun1(w)                 fun2(2)
0x00000076        0x00000076              0x00000076    
0x87654321        0x00000021              0x00000021
0x000000c9        0x000000c9              0xffffffc9
0xEDCBA987        0x00000087              0xffffff87

// 左移24/4=6个十六进制位：只留下最低两位十六进制位
// 右移24/4=6个十六进制位：逻辑移位补0，算数移位补x[w-1]

对一个数取负

对补码的所有位（包括符号位）取反，再 + 1
[-x]补 = ~[x]补 + 1

例子。

1
2
3

x     1 0 1 0    -8+2=-6
~x    0 1 0 1   
~x+1  0 1 1 0    2+4=6

很巧啊，类似，从补码转到原码/从原码转到补码。都是取反+1，不过原码<->补码不涉及符号位。

原码补码转化公式：[x]补 = ~[x]原+1

1
2
3

x     1 0 1 0   -2  这是原码  
~x    1 1 0 1
~x+1  1 1 1 0   -8+4+2=-2   这是x原码对应的补码

所以啊，为什么说在程序中求 -x 就是在求 ~x+1?
- 因为补码及其相反数的转化公式为：**[-x]补 = ~[x]补 + 1**
- 可不是因为原码补码的转化公式是：[x]补 = ~[x]原+1。大一做算法题的时候还误以为是这个原因。

特别的 TMin的相反数是什么？

T Min的相反数还是 T Min
应用公式：[-x]补 = ~[x]补 + 1

假设n=4

3 2 1 0 
0 1 1 1   : T MAX
...
1 0 0 0   : T MIN

~ T MIN
0 1 1 1 
+1
1 0 0 0   = -TMIN

所以

//  1.
x > y 不一定有 -x < -y
当y=T MIN时 y和-y都是最小的

//  2.
x >=0  =>   -x<=0

//  3.
x<=0  !=>   -x>=0
当x=T min时，x=-x=Tmin

如何编写unsigned

该用unsigned吗？
- Java等语言抹去了unsigned，只保留了补码。
  - 但Java中>>是算数右移，>>>是逻辑右移
C标准并没有明确规定有符号溢出会发生什么。我们知识假设是按照补码。但严格意义上我们不能假设C标准以外的东西

提出

size_t i=...;  //size_t : unsigned value of word size
for(i=cnt-2;i<cnt;--i)
{
  a[i]=a[i+1];
}

最终：自己谨慎点吧

所以unsigned这么不好用，什么时候用？

加密算法（需要取模）
仅仅把字看作位的集合，而没有任何数学意义。

无符号数加法

阿贝尔群
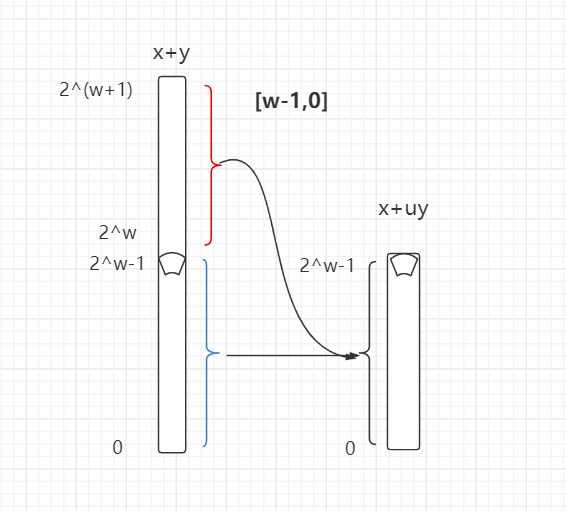
无符号加法公式
- x + w位的无符号数y (写作uwy)
  - = x + y (x+y < 2^w)
  - = x + y - 2^w (2^w <= x+y < 2^w+1)
整数加法和无符号数加法关系。当x+y > 2^w - 1时，和溢出

有符号数（补码）加法

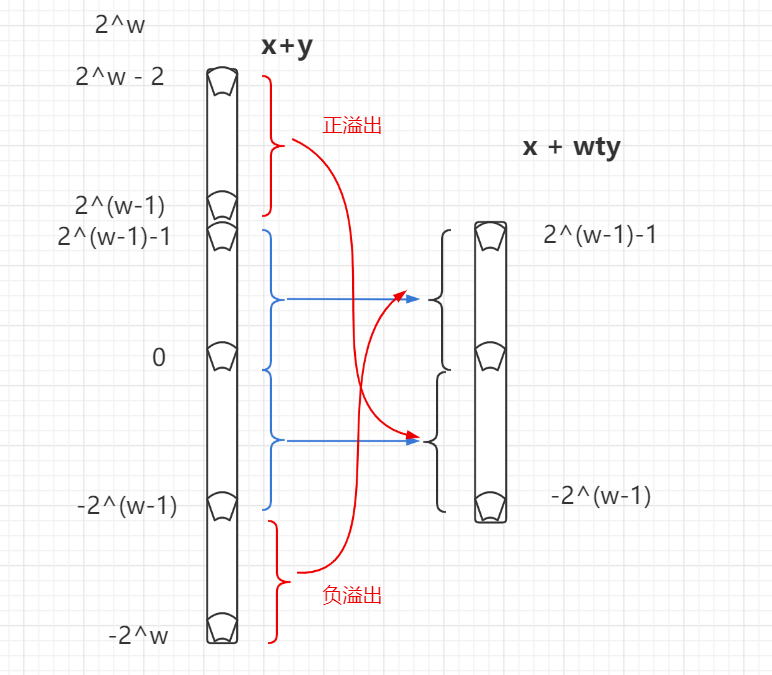
阿贝尔群
补码加法公式
- x + w位的补码y（写作twy）
  - x + y - 2^w （2^(w-1) <= x + y）
  - x + y （ -2^(w-1) <= x + y < 2^(w-1)）
  - x + y + 2^w （ x + y < -2^(w-1)）
整数加法和无符号数加法之间的关系。x + y < 2^(w-1) 时,负溢出； x + y > 2^(w-1)-1时,正溢出

无符号乘法

两个w位的无符号数相乘，结果应当用2w位保存，但是c语言中无符号乘法被定义成产生w位的值，也就是说会截断低位的w位。
将一个无符号数截断为w位，等价于计算该值模2^w
->得到公式： x * uwy = (x*y) mod (2^w)

补码乘法

两个w位的有符号数相乘，结果应当用2w位保存，但是c语言中有符号乘法被定义成产生w位的值，也就是说会截断低位的w位。
将一个无符号数截断为w位，相当于先计算该值模2^w , 再把无符号数转换为补码。
->得到公式：x * twy = U2T ( (x*y) mod (2^w) )

补码乘法和无符号乘法的位级表示是一样的（位级等价性）

无符号除法

除以2的幂
C语言中无符号数x和k
则 x>>k = [x/(2^k)]向下取整

补码除法

除以2的幂
C语言中有符号数x和无符号数k
对于我们编写的x/2^k，则C底层实际实现的是
( x<0 ? x+(1<<k)-1 : x ) >> k
x<0时，需要加上偏置值，这样无论x>0还是x<0，其结果都向0舍入
乘法指令（3个周期）比移位指令（1个周期）花的时间周期多
现代计算机除法仍然很慢 30个周期

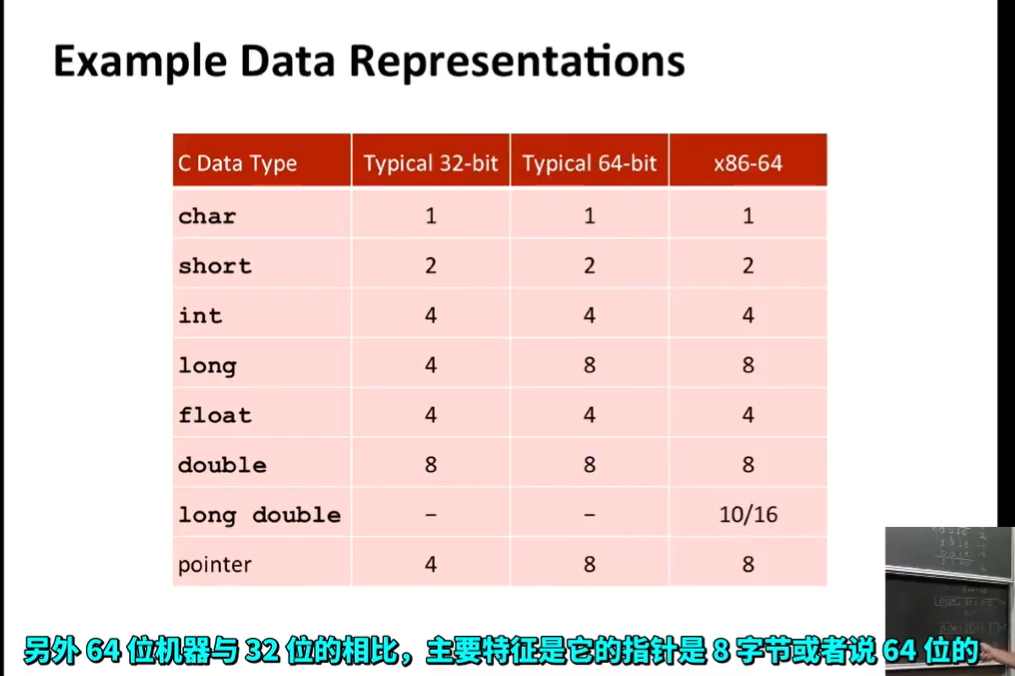
字长

信息存储

64位机器，寻址是2^64。这是逻辑上的。实际上最大是2^48-1。可也正常人没钱买这么大内存。
运行程序时，程序认为他有这么大内存，实际上没有。操作系统只允许他访问能够访问的区域。
机器级程序将内存视为一个非常大的字节数组，称为虚拟内存。
内存的每一个字节都由唯一的数字来标识，称为它的地址。
所有可能地址的集合就称为虚拟地址空间。
- 顾名思义，虚拟地址空间只是一个展现给机器级程序的概念性映像。实际的实现是将动态随机访问存储器(DRAM)、闪存、磁盘存储器、特殊硬件和操作系统软件结合起来，为程序提供一个看上去统一的字节数组。
程序对象：程序数据、指令、控制信息。
- 编译器和运行时系统是如何将存储器空间划分为更可管理的单元，来存放不同的程序对象，即程序数据、指令和控制信息。可以用各种机制来分配和管理程序不同部分的存储。这种管理完全是在虚拟地址空间里完成的。
- 每个程序对象可以简单的视为一个字节快，而程序本身就是一个字节序列
字节顺序：
- 几乎在所有的机器上，多字节对象被存储为连续的字节序列；对象地址为所使用字节的最小地址。
- 大端机器较少，x86机器都是小端，arm处理器既可处理大端也可处理小端，但一般都是小端。
- 基本上只有互联网是唯一一个有大端序的地方。当向网络发送数据包时，会以大端序接收

按字节，将信息以16进制打印（这不是我昨天刚写过类似的吗哈哈哈）

typedef unsigned char* byte_pointer;

void show_bytes(byte_pointer start,size_t len)
{
  size_t i;
  for(i=0;i<len;++i)
  {
    printf("%p\t0x%.2x\n",start+i,start[i]);
  }
  printf("\n");
}

int main()
{
    int a = 9;
    show_bytes((byte_pointer)&a,sizeof a);
    return 0;
}

shc@shc-virtual-machine:~/code/try$ ./a.out 
0x7ffc93b80294  0x09
0x7ffc93b80295  0x00
0x7ffc93b80296  0x00
0x7ffc93b80297  0x00

单位转换

KB MB GB TB
K、M、G、T是数字大小的进制，单位(1)
B是物理意义上的单位，指Bytes

2^10 = 1024 ==10^3

1KB = 1024B = 2^10 Bytes;
1MB = 1024KB = 1024*1024KB = 2^20 Bytes
1GB = 1024MB = 2^30 Bytes = 10^9 Bytes
1TB = 1024GB
1PB = 1024TB = 1125899906842624 Bytes
1EB = 1024PB = 1152921504606846976 Bytes
1MM = 2^20 * 2^20 = 2^40 Bytes = 10^12 Bytes

2^47 估算：
2^40 * 2^7 = 128 * 10^12 Bytes = 128 MM Bytes = 128*10^3 G Bytes

什么是字长

每台计算机都有一个字长，指明指针数据的标称大小。因为虚拟地址是以这样的一个字来编码的，所有字长决定的最重要的系统参数就是虚拟地址空间的最大大小。也就是说，对于一个字长为w位的机器而言，虚拟地址的范围是[0,2^w-1]。程序最多访问2 ^w 个字节。（一个地址背后是1Bytes、8bits的存储空间）
大多数64位机器也可以运行32位机器编译的程序，这是一种向后兼容。我们将程序称为“32位程序”或“64位程序”时，区别在于该程序是如何编译的，而不是其运行的机器类型。
- 生成32位程序，该程序可以在32位/64位机器上运行
  1
  gcc -m32 prog.c
- 生成64位程序，只能在64位机器上运行
  1
  gcc -m64 prog.c
困扰我好久了！这些话解决了大半。
Whatever the largest number is that or the range that sort of signifies how big a pointer is in this language , Or hardware wise the largest sort of chunkof hardware for which.
无论最大数是多少，或者指针表的范围是多少，或者硬件的一个chunk块是多大
There’s a standard support for storing it for arithmetic operations and so forth
有一个标准确定如何存储值和进行算数运算等
So when we say it’s a 64-bit machine
所以当我们说他是64位机器时
What we mean is that it regular and routinely manipulate 64-bit and operations
意思是他惯常处理64位值和算数运算
And also it has a pointer or the values of addresses are 64-bit
并且他的指针和地址的值是64位
Even if for right now only 47 of those bits are usable , it’s still considered a 64-bit machine
即便只有47位是有效的，我们也认为他是64位机器
我们的机器有个奇怪的特性，当我们用gcc作为编译器时，我们可以指定是32位还是64位编译，并且32位和64位会生成两种不同类型的代码。但就目前而言，重点是硬件本身并不一定决定字长的大小，it’s a combination of the hardware and the complier that determines，是由硬件和编译器一起决定的。
- And that code can be run on the point is a 64-bit machine，and can insert of a backward compatibiltiy a style also excutes 32-bit code
And we also saw one of the other feature is
并且我们可以看到另一个特性
Even though it’s a 64-bit word size machine , the data type int without any other qualifiers
即使它是个64位机器：对于数据类型int来说，如果没有任何其他的修饰符
it is jusy 32-bit
它就是32位的
so the sort of this mixture of how big things are
所以这种数据类型大小的定义是混合的
So when people just say word or word size ，
所以当人们说字或者字长时
let’s must say give a precise definition that’s not a very meaningful term
我们必须说。从精确的定义来说，这不是个有意义的术语/措辞
And we’ll sort of throw it around when we mean sort of generic chunk of bits
我们说他的时候一般是泛指一个比特块，
without trying to assume that it has a particular number of bits to it
而不去假设他具有特定数量的bit

64bit的标准int仍然是32位，64位与32位相比，主要特征是64bit的指针是64位的，或者说是8字节的。

习题

p75 经典

记住 无符号数和补码的位级表示相同！！哪怕经过加减乘除计算之后，也仍是这样。（位级别相同的两组补码和无符号数，各自经历相同的加减乘除计算之后，得到的结果的位级表示仍然相同）
记住 -Tmin = Tmin

记住第a位的数在左(右)移b位后，会移动到a+(-)b位上。（数的位数范围[w-1,0]）

// 已知
int x = foo();
int y = bar();

unsigned ux = x;
unsigned uy = y;


(x>0) || (x-1<0)      
//  FALSE
x = Tmin = -2147483648 
则 x<0 , x-1>0

(x&7)!=7 || (x<<29 < 0)
//  TRUE
//  x&7 != 7 ok
//  x&7 == 7 则 x = aaaa...0111
//  则 x<<29 = 111000...0001

(x*x) >= 0
//  FALSE
x = 0xffff
0xffff * 0xffff  = -131071

x<0 || -x<=0
//  TRUE
x = Tmin = -2147483648
-x = Tmin <=0


x>0 || -x>=0
// FALSE
x = Tmin = -2147483648
-x = Tmin <=0

x+y == uy + ux
//  TRUE
补码和无符号数的位级行为相同
也就是说 x + y 与 ux + uy 的位级表示相同
且 在 == 比较时 会将补码转化成无符号数
故 x + y == ux + uy

x*(~y) + uy*ux == -x
// TRUE
~y = -y-1;
x*(-y-1) + uy*ux = -xy -x + uy * ux = -x
补码和无符号数的位级行为相同
也就是说 uy*ux 与 -xy的位级表示相同 。（也许完整的乘积的位级表示可能不同，但是按照C语言标准，截断之后的乘积的位级表示是相同的）（C标准规定截断位w位）
因此 -xy可以和uy*ux相抵消
故 剩下-x

如何计算0xf8

0xf8
1111 1000
高四位的1是符号位扩展出来的，所以：-1 +1 +1 +1 <-> 最低为符号位的-1
-2^4 + 8 = -8

漏洞

csapp p59
习题
- 当length = 0时，会访问非法内存。
  - length = 0，length - 1 = -1 -> UMAX。
  - i先转化成unsigned，然后从0增至UMAX
- 改正：
  - length 类型改为 int。（即便length想要>INT_MAX也没关系，想想就知道了）
  - i <= length - 1 ——> i < length
    1
    2
    3
    4
    5
    6
    7
    8
    float sum_eles(float a[],unsigned length)
    {
    int i;
    float result = 0;
    for( int i=0 ; i<=length-1 ; ++i)
    result += a[i];
    return result;
    }

浮点型

普通的二进制小数

基于此，后来出现了IEEE浮点数表示标准

IEEE浮点数表示（比唐书说得清楚些）

基本规则说明

IEEE浮点标准用 V = (-1)^s * M * 2^E来表示一个数。
- 符号（sign）：1负0正
- 尾数（significand）：M为一二进制小数。范围是 1~2-无穷小 (2^(-n)) 或者 0~1 - 无穷小 (2^(-n))
- 阶码（exponent）：E的作用是对浮点数加权
将浮点数的位表示为三个字段，分别对这三个值进行编码：
- 一个单独的符号位s 直接编码符号s
- k位的阶码字段 exp=ek-1...e1e0 编码阶码E
- n位的小数字段frac=fn-1...f1f0编码尾数M，但是编码出来的值也依赖于阶码字段的值是否等于0。frac每一位的权值为2^-1,2^-2....
图示
- 阶码的值决定了一个浮点数是否是规格化的

是否规格化（三种情况）

V = (-1)^s * M * 2^E
规格化的值：exp的位模式既不全为0，也不全为1。
- E = e-Bias。其中e是无符号数，就是上图中的exp:(ek-1..e1e0)。偏置值Bias=2^(k-1) - 1。（这时候也就是所谓的，用移码方式表示阶码E）
  - 因此，指数的取值范围：单精度 [-126,127] ；双精度 [-1022,+1023]
- M = 1+f。称为隐含的以1开头的表示。
  - 其中f属于[0,1)，f的二进制表示为0.fn-1...f1f0（即小数点在最高位有效位的左边）。因此M可以看为二进制：1.fn-1...f1f0。（可以通过调整E，使得M属于[1,2)。通过M=1+f，使得f不必显示写出那个1。这样，就获得了一个额外的精度位）
非规格化的值：exp的位模式全部为0
- E = 1-Bias
- M = f。即小数字段的值，不包含隐含的开头的1。也即f的值的小数点左侧实际上为0。
- 非规格化数用途
  - 提供了一种表示数值0的方法
    - +0.0：位模式全部为0。s = 0，exp = 0，frac = 0.
    - -0.0：s=1，exp=0，frac=0.
  - 还可用于表示那些非常接近0.0的数
特殊值：exp的位模式全部为1.
- s=0，frac=0，表示正无穷
- s=1，frac=0，表示负无穷
- frac!=0时，其结果表示为 NaN （Not a number）。可用作表示未初始化的数值，或计算结果不能是实数或者无穷。

例子

假设6位浮点格式（3位阶码2位尾数）。可表示的数不是均匀分布的，越靠近远点越稠密
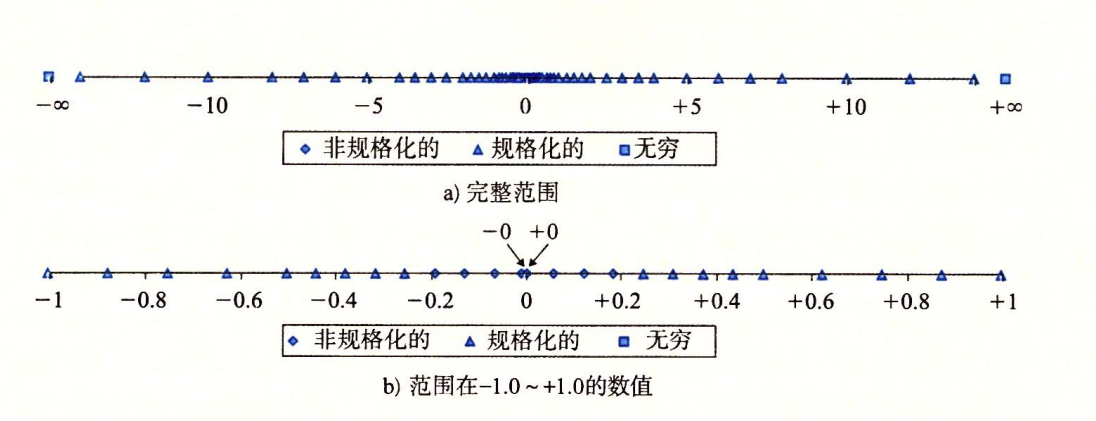
8位浮点格式的非负值示例
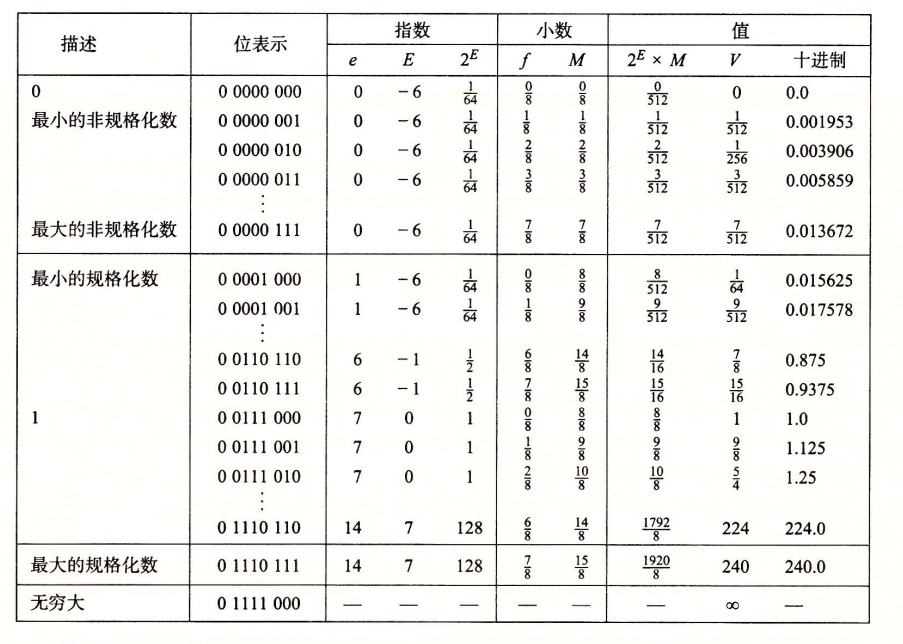
最靠近0：非规格化数。
- E = 1-7 = -6 。权 = 2^E = 1/64
- f = 0，1/8，...，7/8
- 所以V [0,1/64 * 7/8]。（非连续）
- 最小为0
规格化数
- 最小规格化数：
  - E = 1-7 = -6
  - frac = 0,1/8...7/8 -> M = 1+f = 1...15/8
  - 所以V [8/512 , 15/512]
  - 最小为8/512。
- 逐渐增大
- 最大规格化数
  - E = 7
  - frac = 0,1/8...7/8 -> M = 1+f = 1...15/8
  - 所以，最大规格化值 V = 15/8*2^7 = 240
无穷大
- 超过最大规格化数，溢出到正无穷
k位阶码，n位小数的一般规律

整数(int)转化成浮点数(float)表示形式（会改变整数的位）

(unsigned)short、(unsigned)int和(unsigned)long之间转化也会改变位，但是只是进行符号位的(无符号扩展)有符号扩展

int 12345
int的二进制：11000000111001
12345 = (1.1000000111001)2 * 2^13
为了用IEEE单精度形式编码，
构造小数字段：应该丢弃开头的1（作为隐含的1），并在末尾+10个0，来构造小数字段：10000001110010000000000
构造阶码字段：13 + bias（2^(8-1)-1 = 127） = 140。二进制表示为 10001100
再加上符号位0
得到二进制的浮点数表示12345.0(float)
s   exp       frac
0 10001100 10000001110010000000000

convert integer to float图
可以看出 float只有frac的[22,0]位可以用来表示int的数值,因此当int过大时int->float会发生精度损失
- int:[31,0],去掉符号位不算 [30:0],去掉最高位的1不算(因为M = 1+f 1被隐含)就是[29:0],因此如果int的值过大,转为float时会发生精度损失
- int/float转double就一定不会发生精度损失了，因为double的frac是[51:0],能把整个(int)/(float的frac)都涵盖进去
- float/double转int可能会发生溢出。（溢出是看阶码exp，精度损失是看小数位frac）

位级比较
- 12345整形（0x00003039）：
- 12345.0单精度浮点数：（0x4640E400）：

舍入

向上舍入
向下舍入
向0舍入
向偶数舍入
- 向偶数舍入原则有2个
- 当要舍入到的位的之后的位不等于中间值（半值）时，向最靠近的数舍入。也即<半值就向下舍入，大于半值就向上舍入
- 当要舍入到的位的之后的位等于中间值（半值）时，向偶数舍入
  - 如果要舍入到的位，现在是偶数，那么向下舍入，直接舍去后面的位，原先要舍入到的位的数就是舍入的结果。
  - 如果要舍入到的位，现在是奇数，那么向上舍入。
- 例子：舍入到小数点后一位
  - 10.010(2) -> 10.0
    - 因为小数点右边一位的0之后的10 = 0.25 = 0.5/2 ，也即等于半值，所以向偶数舍入，又因小数点后一位为偶数0，所以结果为10.0
  - 10.011(2) -> 10.1
    - 因为 0之后的11 = 0.375 > 0.5/2 ，也即>半值，所以向上舍入，故10.1
  - 10.110(2) -> 11.0
    - 因为小数点右边一位的1之后的10 = 0.25 = 0.5/2 ，也即等于半值，所以向偶数舍入，又因小数点后一位为偶数1，所以(+1向上舍入)结果为11.0
  - 11.001(2) -> 11.0
    - 因为 0之后的01 = 0.125 < 0.5/2 ，也即<半值，所以向下舍入，故10.0
      运算
不是阿贝尔群
- 具备交换律但不具备结合律
赶作业去了

阿贝尔群（近世代数里讲过）

例子

不落辰

CSAPP_2_信息的表示和处理

整形